Of vital importance for faithful color rendition is to take into account the color of the illuminant (incident light) in the scene.

When you put on a pair of colored sunglasses, all that you see becomes temporarily tinted. The same things happen when you enter a room lit by colored lights. From previous experience, the brain knows what colors common objects such as trees and clouds and human skin have and the visual system gradually adapts to the new illumination conditions, and colors seem normal again. The way the brain adapts to different lighting conditions is mimicked in the (automatic) white balance function of digital cameras.

Referring to the CIE chromaticity diagram for the XYZ color system, a collection of points (geometric locus) can be defined that describe the perceived color of a heated black body (a non-reflective black object). The curve formed by these points is known as the Planckian locus.

In essence, as the temperature of the black body increases, the light it emits changes from red to yellow to white and, for very high temperatures, to blue. Upon these observations, the temperature of a color (usually referring to a light source) is defined as the temperature at which heated, the black body emits light of that color. The notion of color temperature is somewhat non-intuitive, because we usually refer to bluish colors as cool and yellow-reddish ones as warm. With color temperature it's the other way around. In the diagram below, the straight lines represent the direction of the colors of equal temperature. All the colors on the, say, 6000K line have the same color temperature but the proportion of green and magenta is what sets them apart. The scale on the right approximately illustrates the color temperature of various common illuminants (light sources).

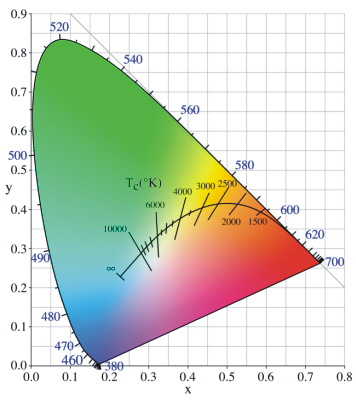
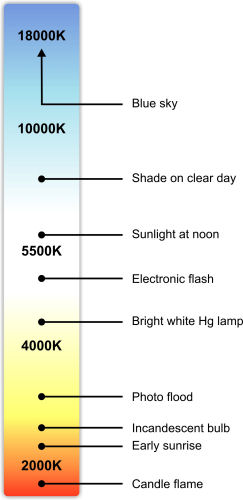
Diagram on left reproduced under GNU public license

In photography the range of illuminants is quite large. Think of the light emitted by a sunset, an overcast sky or a halogen bulb. By what is called white balance the proper compensation for the color of incident light can be applied so that the image will ultimately look like the subject was illuminated by white sunlight (roughly equivalent to 6000 K). There of course cases like shooting neon lights or fireworks, or for special photographic effects, when you would want to keep the color of the incident light, fully or partly.

So what happens when you change the white balance either in camera or from the RAW processing software?

The auto white balance (AWB) function analyses the composition of the scene and compares it to a set of reference metrics stored in the camera's processor and selects the set of parameters most suited to that scene type. The outcome of this process is that the camera will roughly know what scene type it is looking at and what the colors should be. As a consequence it will shift the white point on the Planckian locus and the green – magenta proportion of all the colors to achieve a similarity between the WB corrected image and the internal reference image that it has selected as a model.

Preset white balance settings work in a similar fashion except that the scene is not analyzed, but instead the colors and the white point are shifted using predefined values.

That ‘set white balance feature' present on a large number of cameras lets the user effortlessly create a white balance profile to match the exact lighting conditions. What is needed is a white or neutral grey (preferably non-reflective) card lit by the respective illuminant that the camera while measure. This essentially involves holding the card in front of the lens so that it covers the center of the image and pressing the set white balance or equivalent button. The camera will then analyze the image (and the color it will see will most probably not be pure grey but it will rather be a more or less saturated hue) and compensate so that after processing the patch will look grey. This method of achieving proper white balance yields remarkably good results due to the fact that it completely removes the influence of the colored incident light, effectively making the picture look as if the scene was illuminated by noon sunlight (white light).

Achieving proper white balance in a scene in which multiple light sources of different types (color temperatures) are present can be quite tricky but at the same time these scenes are quite spectacular subjects. As an example, the following picture of below average artistic value of a fairly known piece of white marble illustrates how white balance can change the look and mood of an image.

To the right and back of Venus was a window that let in white sunlight and the reflector light was quite orange. By choosing white balance setting that turned the yellow light whiter, the proper white light illuminating the background was made bluer. Of course, tastes vary, but in general, a white sculpture with a bluish background is more appealing than a yellow tinted sculpture on a white background.

Most problems with white balance appear because in many cases incident light does not come from a black body heated to incandescence (e.g. the Sun). The assortment of lighting fixtures that give of white-ish light we have today have a discrete band emission spectrum. The incident light might also be reflected from colored surfaces. All this implies a greenish or magenta deviation from the Plankian locus. The purpose of the tint control in most RAW converters is to enable the photographer to compensate for this deviation in addition to changing the color temperature. As it is, in- camera AWB algorithms might be very suited for some lighting situations but terrible at handling others.

When color goes digital

The light spectrum is infinitely divisible, meaning that if you chose two spectral colors, there are an infinite number of colors between them. When it comes to color representation that poses a problem and, as no-one is seriously thinking about storing an infinite amount of data, unnecessary complexity needs to be removed. For digital systems, this is done by sampling the color space, turning it from a continuous space to a discrete one.

Considering MacAdam distances (discrete colors should not be farther apart than the minimum perceivable difference) and storage requirements, it was concluded that 16.7 million discrete colors across a RGB color space would be enough. This number is in fact in 2^24, or more precisely 2^(8+8+8) with each 8 standing for 8 bits of data for each primary color.

We refer to the number of discrete colors that a color space is divided in as color depth. In the above case (which is the norm for digital images), the color depth is 8-bit or alternatively 24-bit (3 times 8).

8-bit color depth is quite adequate for most capture-store-display situations where sRGB is used. When working with larger gamut color spaces keeping the same color depth results in larger granularity. This in turn might lead to posterization (the transformation of uniform gradients to tonal steps), which can also occur when aggressively manipulating images in small-gamut spaces. At the expense of memory and processing power, colors can be represented with 16 bits per channel, resulting in a color depth of 16 bits (or 48 bits). By working with an extended color depth, the above effects are all but eliminated.

To show the limitations of 8-bit color, the example below illustrates how a large-gamut and a small-gamut imaginary color space would be chopped into discrete colors using 8-bit and 16-bit precision. The differences are exaggerated to prove the point.

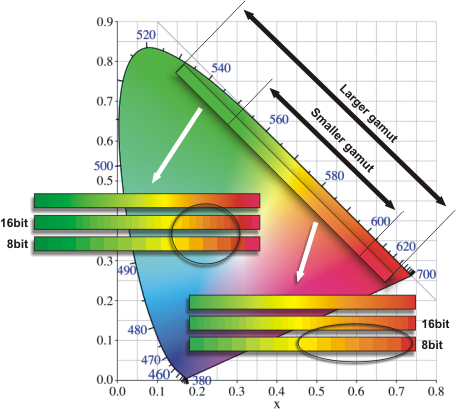
Suppose that the image of interest contains a sunset with lots of close orange shades. When working with the narrow-gamut color space and 8-bit depth, there are plenty of orange shades. Let us assume that there are enough of them so that no posterization occurs.

If we keep the 8-bit color depth but switch to the larger-gamut color space, the range of oranges is immediately reduced because more bits are needed to represent greens and reds. In order to achieve the same gradation for our orange shades, we need to switch to 16-bit depth. The example also shows that switching to 16-bits in the smaller-gamut space does not improve the situation.