|
© by
This e-mail address is being protected from spambots. You need JavaScript enabled to view it
unless noted otherwise - exclusivly licensed to opticallimits.com
Digression on how we measure
colors
Colors are identified by their
characteristics. These are:
- Color hue, the essential quality which
differentiates colors.
- Luminance; allows classification in relation
with an achromatic (grey) scale – we say that the color is light or dark.
- Saturation or purity. The pure colors are the colors found in the spectrum
(and on the edge of the chromaticity diagram). By drawing an imaginary line
between the reference monochromatic radiation (white) and any color, we can
judge the purity of a color by the distance from the pure color (the closer, the
purer)
Again Colorimetric
Systems
With these properties in mind, here are some more
interesting facts about the CIE-XYZ color space:
- When mixing two
colors, the resulting color is placed on the imaginary line between the two
original ones. Its placement on this line is in accordance with the ratio of the
two original colors.
- Colors which when mixed result in the color E
(reference white) are called complementary
|
The
CIE-XYZ contains an infinite number of colors and those that are very close to
each other in the diagram are highly alike. The ‘distance' between two colors
represents the similarity between them. The closer they are, the more they look
the same. But the human visual system can only distinguish two colors as being
different if they are slightly apart. The minimum distance between two colors
for which the ‘average human observer' can still tell them apart is called the
MacAdam distance. For any given color in the CIE-XYZ space, there is an area
(MacAdam ellipse) surrounding that particular color containing colors that are
perceived as being the same as the original color. Since the human visual system
is sensitive in different degrees to red, green and blue, the MacAdam ellipses
vary in shape and area depending on the location in the color space. A rough
representation of the MacAdam ellipses for several colors in the CIE-XYZ color
space is shown below. The area of the ellipses is highly exaggerated in order to
illustrate the concept.
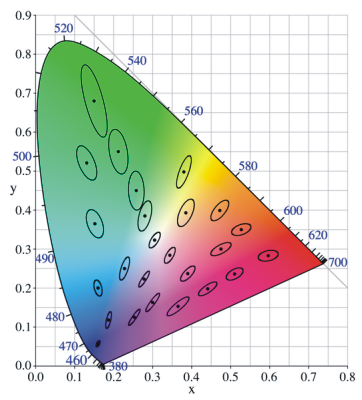
Image reproduced under GNU
public license
A more ‘perceptual' representation of the CIE-XYZ
color space can be obtained by reshaping it so that the MacAdam ellipses are in
fact circles that all have the same area. This was attempted with more
contemporary CIE diagrams, but the XYZ remains the standard.
|
On Color Spaces
|
Having defined the CIE-XYZ colorimetric system, we can
discuss color spaces.
A color space is the sum of all the colors that
can be represented starting from a set of primaries and a blending (color
mixing) rule. Moreover, it is a mathematical description of how colors can be
uniquely identified by a suite of values called color components. Forcing the
definition, the CIE-XYZ colorimetric system is in itself a color space (the
color space of human color vision). All color spaces within the CIE-XYZ are
three dimensional spaces and the horseshoe diagram is a slice in the CIE-XYZ
color space for maximum z (maximum brightness). In the CIE-XYZ-derived color
spaces, the rule is additive mixing.
To create a color space (a subspace)
in the CIE-XYZ, any number of primaries can be used. Within the chromaticity
(horseshoe) diagram, a color space would look like a polygon with the primaries
as its tips.
The area of the polygon for a particular color space is
called the gamut of that space. The bigger the gamut, the larger the number of
colors contained.
Any useful color space would include the white point,
and the simplest ones to describe only use three primaries. Since you can only
obtain a triangular area using three primaries and the horseshoe is far from
being triangular, many colors will be inevitably left out of any three-primary
color space.
For an analogy with the human visual system the primaries
can be red, green and blue. The chromaticity diagram contains many reds, greens
and blues, so different color spaces can be created. The primaries can be chosen
from all the colors, but by choosing very saturated primaries (i.e. peripheral
colors), the resulting color space will obviously include more saturated colors.
|
RGB color
spaces
All the RGB spaces have in common the three parameters
used for describing a color, namely the amounts of primary red, green and blue
(color coordinates). For any particular color, if the primaries (i.e. the color
space) are changed, the color coordinates of the color will be different; the
color stays the same, the reference system changes. Hence, the need of proper
techniques for changing color spaces.
The default color space is sRGB. It
is the standard for web browsers and virtually all consumer cameras and has a
gamut covering roughly one third of the visible colors, and lacking particularly
in the ability to represent very saturated cyan, green and to some extent,
yellow.
AdobeRGB (1998) is an extension of the sRGB color space. The red
and blue primaries are kept from sRGB but the green primary is shifted to a more
saturated color, resulting in the capacity to represent more (and in particular
more saturated) shades of green and cyan. AdobeRGB has a wider gamut than sRGB
and it contains around 50% of the colors in the chromaticity diagram. Although
sRGB is included in AdobeRGB, converting between the two spaces may raise some
problems if not done properly; more on that in the last part of this
article.
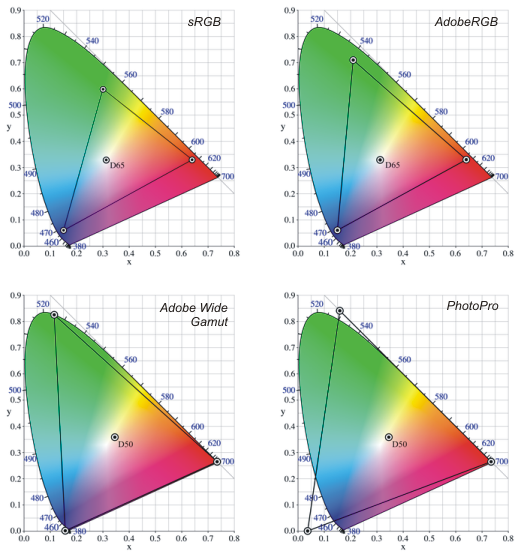
Image adapted under GNU public
license
|
Still wider is the Adobe Wide Gamut color space. All three
primaries are fully saturated and the gamut is almost 80% of the visible colors.
This color space is not widely used and, because of the very wide gamut,
justifies using a 16bit color depth per channel. Bit depth will also be
discussed further.
An even wider color space is called PhotoPro which
uses a spectral red but imaginary (not present in the chromaticity diagram) blue
and green primaries. It can represent just over 90% of the real colors but it
contains around 13% virtual colors that cannot be represented on any medium
(wasted bits).
|
The figure below exemplifies how
the proportions of red, green and blue affect the look of a color. A reference
color (‘perforated' patch) was selected, its R, G and B proportions being
unequal (otherwise it would have been grey).

The diagram shows the
effects of keeping two color components constant while varying the other in
steps of ~ 12.5%
CMYK
The RGB
color spaces described above additively mix the primaries to obtain the desired
color. Subtractive mixing uses mainly cyan, magenta and yellow as primaries and
is generally used for white media (i.e. printing). It is interesting to observe
that taking any RGB color space (triangle in the chromaticity diagram), the
cyan, magenta, and yellow colors are situated (roughly) halfway between two RGB
primaries on the sides of the triangle. CMY color spaces generally have a
smaller gamut than the sRGB color space, particularly because that they do not
contain very dark saturated colors. Subtracting fully saturated C, M and Y from
white at the same time does not create black. This is the reason black is
usually added as a primary. It is abbreviated K from ‘key'. A serious problem
arising when converting from RGB to CMYK (which happens whenever you print
something digital) is represented by the fact that, generally speaking, there
are colors in RGB that are not present in CMYK and vice versa.
Just as
with the RGB example, the figure below demonstrates the effect of altering the
amount of one color component while keeping the other three unchanged. On each
line the colors are about 12.5% apart in terms of the proportion of C, M, Y and
K respectively.

The ‘reference' color (again the perforated patch) occupies
a different position on each row because of the different proportions of C, M, Y
and K present within it (it has less cyan than it has magenta etc).
|