|
Viltrox PFU RBMH 85mm f/1.8 STM (Fujifilm X) - Test Report / Review - Analysis |
|
Lens Reviews -
Fujifilm X
|
|
Page 2 of 3
Distortion
Unlike many Fujinon lenses, the Viltrox PFU RBMH 85mm f/1.8 STM is fully corrected thus it produces a very low native distortion (pincushion-style) of just 0.3%
Vignetting
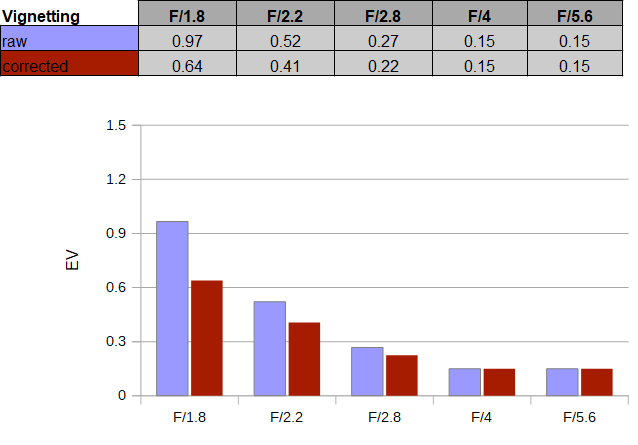
As mentioned in the introduction, the Viltrox lens is actually capable of covering a full-format image frame. So does it have an easy play on Fujifilm's APS-C format sensor when it comes to vignetting?
While the light falloff is reasonably well-controlled at f/1.8, you will still be able to spot a light falloff of 0.9EV (f-stops) in critical scenes. If you use activated image auto-correction, it is a bit less than that. The issue is substantially reduced at f/2.2 and negligible from f/2.8 onward.
MTF (resolution)
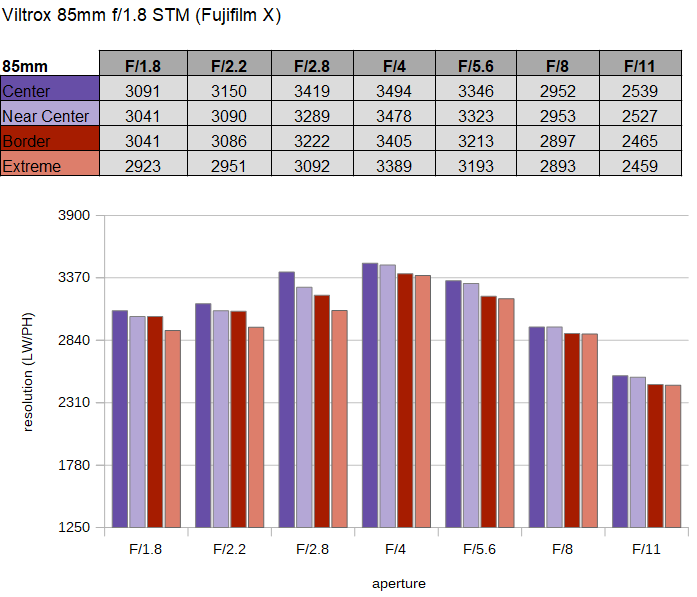
Starting with this review, we have moved to a 26 megapixels camera for the tests. The charts scale was calibrated using the Fujinon XF 90mm f/2 R LM WR.
The resolution characteristic of the Viltrox PFU RBMH 85mm f/1.8 STM is very decent. While the Viltrox lens can't touch the peak performance of the Fujifilm 90mm f/2, it is capable of reaching a very good image quality straight at f/1.8. Stopping down to f/2.2 has little effect but the quality improves at f/2.8 and reaches excellent (just) levels at f/4 - across the image frame. Diffraction is limiting the resolution beyond with a somewhat noticeable impact at f/8. f/11 should be avoided if possible.
The field curvature is marginal. The centering quality of the tested sample was good.
Please note that the MTF results are not directly comparable across the different systems!
Below is a simplified summary of the formal findings. The chart shows line widths
per picture height (LW/PH) which can be taken as a measure for sharpness.
If you want to know more about the MTF50 figures you may check out the corresponding
Imatest Explanations
Chromatic Aberrations (CAs)
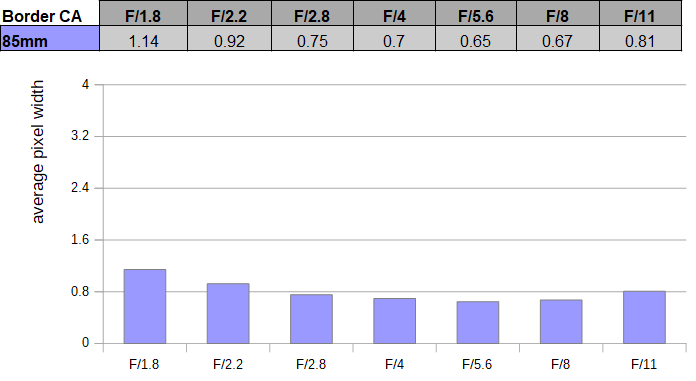
Lateral CA (color shadows at the image borders) are well controlled with an average pixel width peaking at 1.1px mark at the image borders at f/1.8. The CAs are lower and quite negligible at medium aperture settings.
Bokeh
If you decide to buy a fast prime lens, you also do so for superior bokeh compared to the zoom lenses - and the Viltrox lens delivers nicely in this respect.
Out-of-focus highlights are beautifully rendered in the image center with no outlining and a very smooth inner zone. Stopping down maintains the highlight circle at f/2.2 but you can spot the edgy aperture shape from f/2.8 already.
The images below illustrate the deterioration of the out-of-focus highlights towards the image corners. The circular shape is kept across a quite broad image field but you can clearly spot "cat eyes" in the image corners at f/1.8 - a vignetting effect. The corner highlight shape improves quite a bit when taking shots at f/2.8 as you can notice below.
The general rendition in the focus transition zones is excellent with very smooth edge transitions both in the image background (shown to the left below) as well as in the foreground (to the right).
Bokeh Fringing (LoCA)
Bokeh fringing - also referred to as LoCAs - is a color fringing effect on the Z-axis. It shows up as purplish halos in front of the in-focus zone and greenish beyond. The effect is visible at f/1.8 albeit it is not extreme. Stopping down to f/2.2 reduces the fringing and there are traces left at f/2.8. The LoCAs are mostly gone from f/4 onward.
Keep in mind that bokeh fringing is normal in all but a handful of very expensive APO lenses.
|
