|
Canon EF 50mm f/2.5 macro - Review / Test Report - Analysis |
|
Lens Reviews -
Canon EOS (APS-C)
|
|
Page 2 of 3

Distortion
As expected for a fix-focal lens and especially for a macro lens the level of distortion is absolutely
negligible:

The chart above has a real-world size of about 120x80cm.
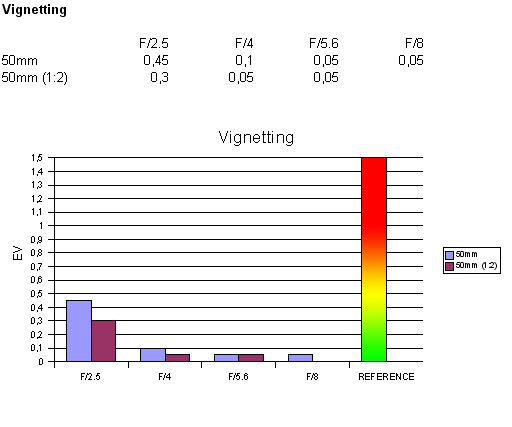
Vignetting
On the EOS 350D with its reduced format (APS-C) the lens exhibits little vignetting. At f/2.5 vignetting
may be visible in very critical scenes but at f/4 the degree is already negligible. More so at close-focus
distances where vignetting is even less pronounced. Expect more vignetting on 1.3x or full frame cameras.
MTF (resolution & chromatic aberrations)
Typical for most macro lenses the EF 50mm f/2.5 performed excellent in the lab. The lens is already very good
in the center at wide-open aperture though the borders suffer a little here. From f/4 & up the border performance
is almost as good as the center. The lens reaches its peak performance at f/5.6 where is scratches or even
exceeds the resolution limits of the 8 megapixel sensor of the EOS 350D. Beyond diffraction effects limit
the performance - something that can't be avoided. The lens provides an extremely min. aperture setting of
f/32 but the quality suffers quite a bit here. Unless you really need the extra bit of depth-of-field you should
stay at or below f/16.
Please note that the MTF results are not directly comparable across the different systems!
Below is a simplified summary of the formal findings. The chart shows line widths per picture height (LW/PH) which can be taken as a measure for sharpness.
If you want to know more about the MTF50 figures you may check out the corresponding Imatest Explanations
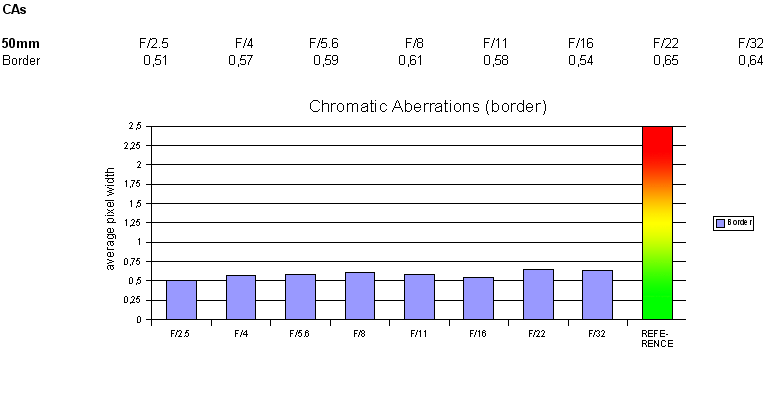
Chromatic Aberrations (CAs)
Similar to most other fix-focal lenses chromatic aberrations (color shadows at harsh contrast transitions) are
very low and usually nothing to worry about.
|